Si deseas una ASESORÍA VIRTUAL O PRESENCIAL puedes contactarme a través de mi correo christianjgutierrezr@hotmail.com o través de los telefonos (0426)-185.69.03 (0414)-847.64.72 (0293)-452-26.76
No es un número, es una expresión que hace referencia a una cantidad sin límite o sin final.
EL NÚMERO CERO (0)
Es el signo numérico de valor nulo, una expresión que se interpreta como: nada, nadie, ninguno, etc. Es un número con el cual se pueden realizar operaciones algebraicas como sumas, restas, multiplicación, entre otras, pero que en ocaciones puede dar lugar a expresiones indefinidas, indeterminadas o que carecen de sentido.
El cero, por ser un concepto numérico especial, no se incluía en el conjunto de los números naturales ℕ, por ello es posible encontrar muchos libros donde los autores no consideran al cero como número natural. De hecho, aún no hay consenso al respecto. Algunos matemáticos lo consideran perteneciente al conjunto de los naturales ℕ ya que estos también se pueden definir como el conjunto que nos permite contar el número de elementos que contienen los demás conjuntos, y el conjunto vacío tiene ningún elemento.
DIVISIÓN POR CERO
En los números naturales, enteros y reales, la división por cero no posee un valor definido, debido a que para todo número n, el producto n·0 = 0, por lo que el 0 no tiene inverso multiplicativo. En otros cuerpos matemáticos, pueden existir divisores de cero, sin embargo, estos aparecen cuando el cero es el dividendo, no el divisor.
Si recordamos la división, en el sentido de reparto ya que es claramente el más intuitivo, donde el divisor es necesariamente un número entero; suponiendo que queremos repartir 20 peras entre 4 personas tendríamos la expresión 20/4 lo cual nos da un total de 5 peras que es lo que le toca a esas 4 personas. Esto nos sugiere que las expresiones 20/0 y 0/0 carecen de sentido. Intuitivamente, significa que no tiene sentido repartir 20 peras entre cero personas. Tampoco tiene sentido, distribuir 0 peras entre cero personas.
Desde el punto de vista del análisis matemático, la indefinición de una división por cero puede solventarse mediante el concepto de límite.
Sin embargo, aunque aparentemente aceptable en la práctica, esta solución (división por cero es igual a infinito) puede generar paradojas matemáticas, conocidas como diferentes infinitos.
EL INFINITO
No es un número, es una expresión que hace referencia a una cantidad sin límite o sin final.
Veamos un ejemplo creativo para entender por qué la división por cero es infinito:
Una freidora tiene una capacidad de 6 litros de aceite. Si la llenamos con botellas de 1 litro, necesitamos exactamente 6 botellas, si la llenamos con botellas de medio litro (500ml), necesitamos 12 botellas. Si las botellas son de 0,2 litros (200ml), necesitamos 30 botellas y así, a medida que la capacidad de la botella es menor, se requieren más botellas.
Es evidente que las botellas de capacidad cero no existen, ¿verdad? ¿Cómo vas a llenar sin echar nada? Pero imagínate que las botellas son de 0,01 l (10ml). Necesitaríamos nada menos que 600 botellas. Pero más pequeño aún, cada botella es una gota de aceite, ¿cuántas gotas hacen falta para llenar la freidora? La respuesta es evidente, ¿verdad? Muchísimas, podría decirse INFINITAS.
OPERACIONES CON INFINITO
Debemos tener claro que las siguientes indicaciones no son operaciones propiamente dichas, sino simplemente un recurso (reglas nemotecnias) para ayudarnos a resolver límites.
FORMAS INDETERMINADAS
Ya habíamos mencionado que la división por cero donde el numerador tambien es cero es una indeterminación, pero ¿qué significa esto?, pues significa que no sabemos exactamente cuál es el resultado de dicha expresión puede ser cualquier cosa. Puede ser 0, puede ser ∞, puede ser 1, puede ser 14, puede ser...
Generalmente la indeterminación 0/0 la encontramos cuando estamos resolviendo límites de funciones racionales. Para resolver este inconveniente (levantar la indeterminación) tenemos que conseguir simplificar la fracción, y para ello hemos de conseguir factorizar los polinomios del numerador y denominador. Una vez hecho esto y simplificada la expresión, la indeterminación habrá desaparecido y se podrá calcular el límite.
Nota: Para cada tipo de indeterminación que aparezca cuando estamos resolviendo límites se tiene un procedimiento diferente para levantar dicha indeterminación.





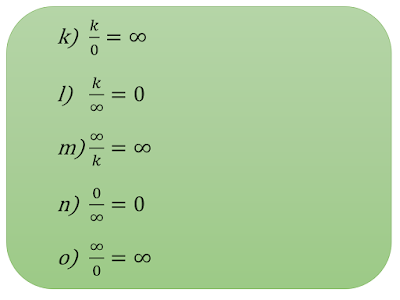


Estmado, y que pasa con infinito por cero?, espero me respondas en ese caso te lo agradezco de antemano
ResponderBorrarEs una indeterminación. Ve los casos de indeterminacion en la ultima imágen
ResponderBorrarEn ese caso lo mejor que se puede hacer es transformar esa indeterminacion ceroxinfinito en indeterminacion infinito/infinito ó tambien en cero/cero que sabemos como proceder
ResponderBorrar